Softmax activation function for AI/ML engineers

In the field of machine learning and deep learning, activation functions play a key role in the ability of neural networks to make complex decisions and predictions. Among them, the softmax activation function stands out, especially in classification tasks where the outcomes are mutually exclusive. This article delves into the softmax function, offering insight into its operation, applications, and significance in the field of artificial intelligence (AI).

Softmax activation function

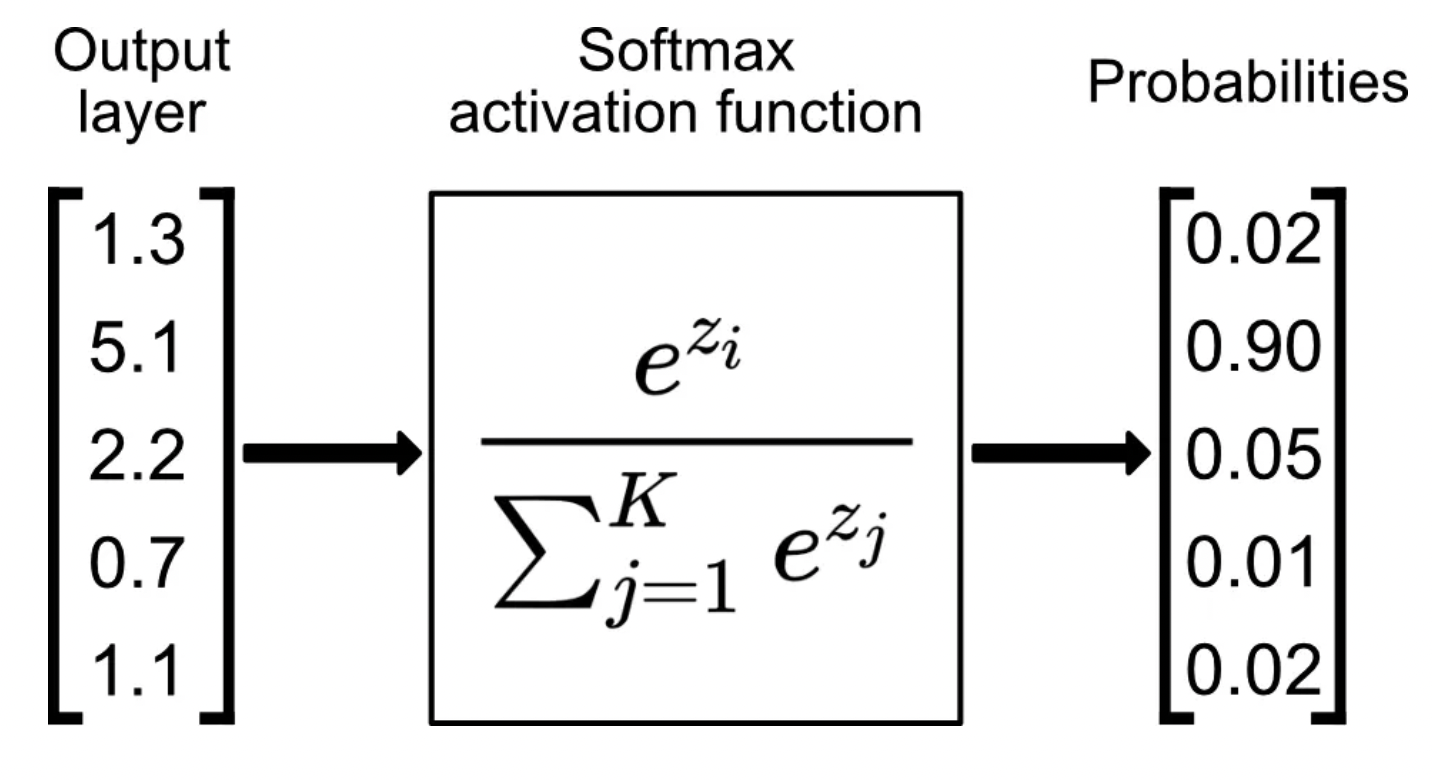
Image authors: Towards data science

The softmax function, often used in the final layer of neural network models for classification tasks, converts raw outputs—also known as logits—into probabilities by taking the exponential of each output and normalizing those values ​​by dividing by the sum of all exponentials. This process ensures that the output values ​​are in the range (0,1) and sum to 1, making them interpretable as probabilities.

The mathematical expression for the softmax function is as follows:

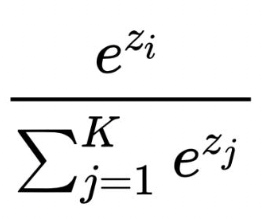
Here, zi represents the input to the softmax function for class i, and the denominator is the sum of the exponentials of all the raw results of the class in the output layer.

Imagine a neural network tasked with classifying images of handwritten digits (0-9). The final layer can print a vector with 10 numbers, each corresponding to a digit. However, these numbers do not directly represent probabilities. The softmax function goes into converting this vector into a probability distribution for each digit (class).

Here’s how Softmax achieves this magic

1. Input: The softmax function takes a vector z of real numbers, which represents the outputs from the final layer of the neural network.
2. Potentiation: Each element uz is exponentiated using the mathematical constant e (approximately 2.718). This ensures that all values ​​become positive.
3. Normalization: The weighted values ​​are then divided by the sum of all weighted values. This normalization step guarantees that the output values ​​sum to 1, which is a key property of the probability distribution.

Properties of the Softmax function

• Output range: The softmax function guarantees that the output values ​​lie between 0 and 1, satisfying the definition of probability.
• Sum of probabilities: As mentioned earlier, the sum of all outputs from the softmax function is always equal to 1.
• Interpretability: Softmax transforms raw results into probabilities, making network predictions easier to understand and analyze.

Applications of Softmax activation

Softmax is predominantly used in multi-class classification problems. From image recognition and natural language processing (NLP) to recommendation systems, its ability to efficiently handle multiple classes makes it indispensable. For example, in a neural network model that predicts types of fruit, softmax would help determine the probability that the image is an apple, orange, or banana, ensuring that the sum of these probabilities is equal to one.

In Python, we can implement Softmax as follows:

from math import exp

def softmax(input_vector):
    # Calculate the exponent of each element in the input vector
    exponents = [exp(i) for i in input_vector]
    
    # Correct: divide the exponent of each value by the sum of the exponents
    # and round off to 3 decimal places
    sum_of_exponents = sum(exponents)
    probabilities = [round(exp(i) / sum_of_exponents, 3) for i in exponents]
    
    return probabilities

print(softmax([3.2, 1.3, 0.2, 0.8]))

The output will be:

Comparison with other activation functions

Unlike functions such as sigmoid or ReLU (Rectified Linear Unit), which are used in hidden layers for binary classification or nonlinear transformations, softmax is uniquely suited for the output layer in multi-class scenarios. Although the sigmoid compresses the outputs between 0 and 1, it does not ensure that the outputs sum to 1 — making softmax more suitable for probabilities. ReLU, known for solving vanishing gradient problems, does not provide probabilities, emphasizing the role of softmax in the context of classification.

Softmax in action: Multi-class classification

Softmax shines in multi-class classification problems where the input can belong to one of several discrete categories. Here are some real-world examples:

• Image recognition: Classifying images of objects, animals or scenes, where each image can belong to a certain class (eg cat, dog, car).
• Spam detection: Classifying emails as spam or not spam.
• Sentiment Analysis: Classifying the text into categories such as positive, negative or neutral opinion.

In these scenarios, the softmax function provides a probabilistic interpretation of network predictions. For example, in image recognition, the softmax output might mean a 70% probability that the image is a cat and a 30% probability that it is a dog.

Advantages of using Softmax

There are several benefits of using the softmax activation function — here are a few that you can benefit from:

• Probability distribution: Softmax provides a well-defined probability distribution for each class, which allows us to estimate the confidence of the network in its predictions.
• Interpretability: Probabilities are easier to understand and communicate compared to raw output values. This allows better evaluation and debugging of the neural network.
• Numerical stability: The softmax function shows good numerical stability, which makes it effective for training neural networks.

Guide for activating the Softmax function

Let’s see how the softmax activation function works through a simple tutorial.

Let’s use the SingleStore Notebook feature to perform this tutorial. If you haven’t already, activate a free trial of SingleStore to start using laptops.

After signing in, go to the ‘Develop’ option and create a blank notebook.

Name your notebook and start adding the following instructions.

The textbook illustrates the calculation of the softmax likelihood from a set of logits, showing its application in converting the raw scores to probabilities that sum to 1.

Step 1: Install the NumPy and Matplotlib libraries

!pip install numpy
!pip install matplotlib

Step 2: Import the libraries

import numpy as np
import matplotlib.pyplot as plt

Step 3: Implement the Softmax function

Implement the softmax function using NumPy. This function takes a vector of raw scores (logits) and returns a vector of probabilities.

def softmax(logits):

    exp_logits = np.exp(logits - np.max(logits))  # Improve numerical stability

    probabilities = exp_logits / np.sum(exp_logits)

    return probabilities

Step 4: Create a set of logits

Define the logit set as a NumPy array. These logits can be raw scores from any model output that you want to convert to probabilities.

logits = np.array([2.0, 1.0, 0.1])

Step 5: Apply the Softmax function

Use the softmax function defined earlier to convert the logit to a likelihood.

probabilities = softmax(logits)
print("Probabilities:", probabilities)

Step 6: Visualize the results

To better understand the effect of the softmax function, visualize the logits and resulting probabilities using Matplotlib.

# Plotting
labels = ['Class 1', 'Class 2', 'Class 3']
x = range(len(labels))

plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.bar(x, logits, color="red")
plt.title('Logits')
plt.xticks(x, labels)

plt.subplot(1, 2, 2)
plt.bar(x, probabilities, color="green")
plt.title('Probabilities after Softmax')
plt.xticks(x, labels)

plt.show()

The full tutorial code can be found here in this repository.

The softmax function is an essential component of neural networks for multi-class classification tasks. It allows networks to make probabilistic predictions, enabling a more nuanced understanding of their results. As deep learning continues to evolve, the softmax function will remain a cornerstone, providing a bridge between the raw computations of neural networks and the world of interpretable probabilities.